플로이드-와샬 알고리즘 Floyd-Warshall Algorithm

플로이드-와샬 알고리즘

모든 정점 사이의 최단 거리를 찾는 알고리즘.

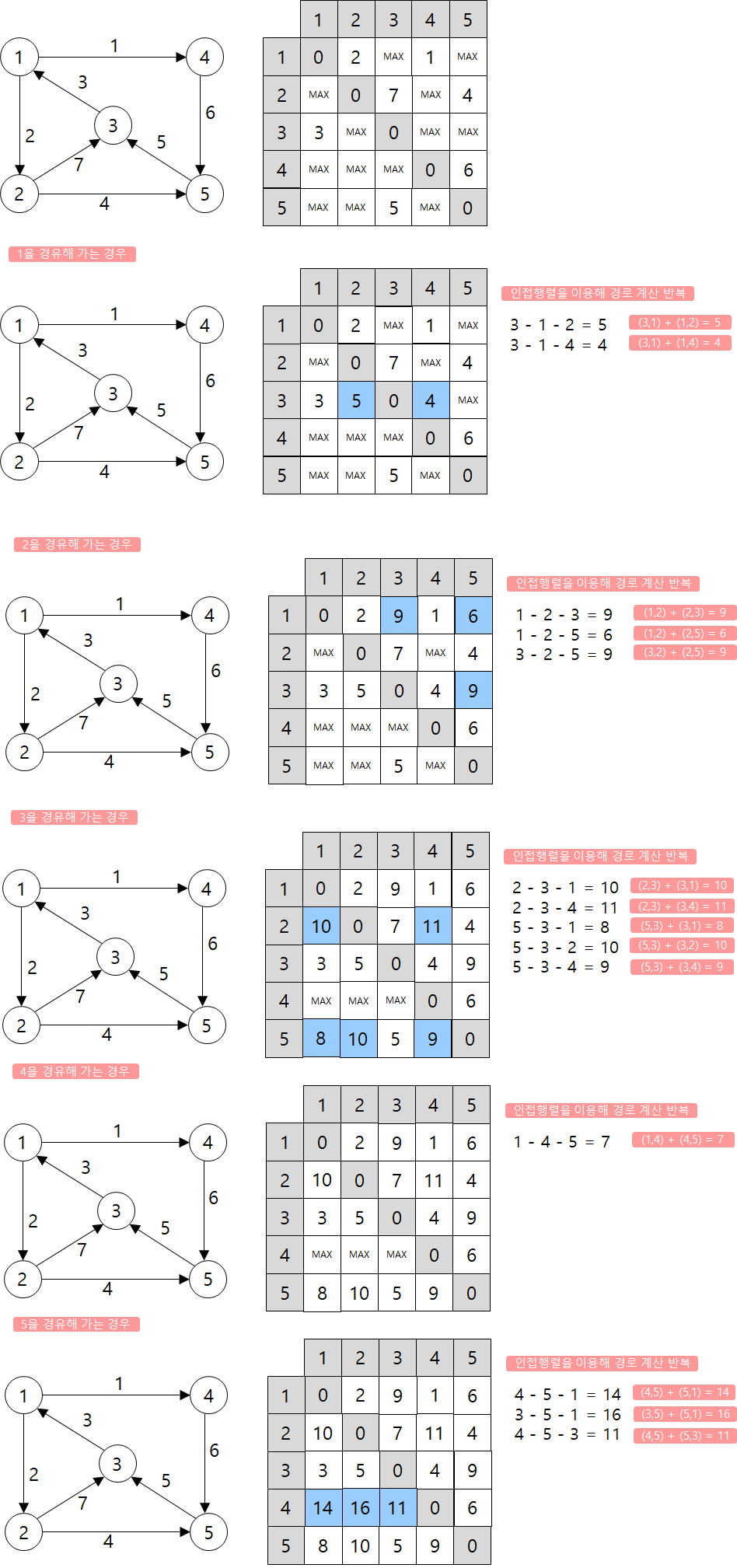
그래프를 인접행렬로 표현한다.

정점마다 경로 가중치를 기록한 인접행렬을 탐색하여 최단경로를 찾는 방식이다.

 

슈도코드

① 인접행렬 A 생성 

② for ( k  to 정점갯수) {

          for ( i  to 정점갯수) {

                for ( j  to 정점갯수) {

                   //현재 경로 값과 정점 K를 거쳐가는 경로 값을 비교하여 더 작은 값을 저장  

                     if (A ( i , j )  > A ( i , k ) + A( k , j ) ) {

                                 A ( i , j ) = A ( i , k ) + A( k , j );

                     }      

                } 

           } 

    } 

 

시간복잡도

① 정점 K를 거쳐가는 경로를 탐색

② ①을 수행할 때마다 경로 가중치를 기록한 인접행렬 V²을 탐색

O(V³)

 

구현 JAVA

package test;

import java.util.Arrays;

public class floyd {
	
	public static void main(String[] args) {

		//그래프 선언
		int max = Integer.MAX_VALUE;
		
		int[][] graph = {{0,2, max , 1, max},
						{max, 0, 7, max, 4},
						{3, max, 0, max, max},
						{max, max, max, 0, 6},
						{max, max, 5, max, 0}};
		//결과 출력
		for(int[] row : graph ) {
			System.out.println(Arrays.toString(row));			
		}
		
		// 플로이드 알고리즘 실행
		floyd f =  new floyd();
		f.floyd(graph);
		
		System.out.println("결과값 출력");
		//결과 출력
		for(int[] row : graph ) {
			System.out.println(Arrays.toString(row));			
		}
	}

	
	void floyd(int[][] graph) {
		
		int nodeCount = graph.length;
		
		for(int k = 0; k<nodeCount; k++) {
			for(int i = 0; i<nodeCount; i++) {
				for(int j = 0; j<nodeCount; j++) {
					if(graph[i][k] < Integer.MAX_VALUE && graph[k][j] < Integer.MAX_VALUE) {
						if(graph[i][j] > graph[i][k]+graph[k][j]) {
							graph[i][j] = graph[i][k]+graph[k][j];
						}
					}
				}
			}	
		}
	}
}

 

출처

• 컴퓨터 알고리즘 기초 18강 플로이드-와샬 알고리즘, T아카데미
• Floyd-Warshall Algorithm, programiz